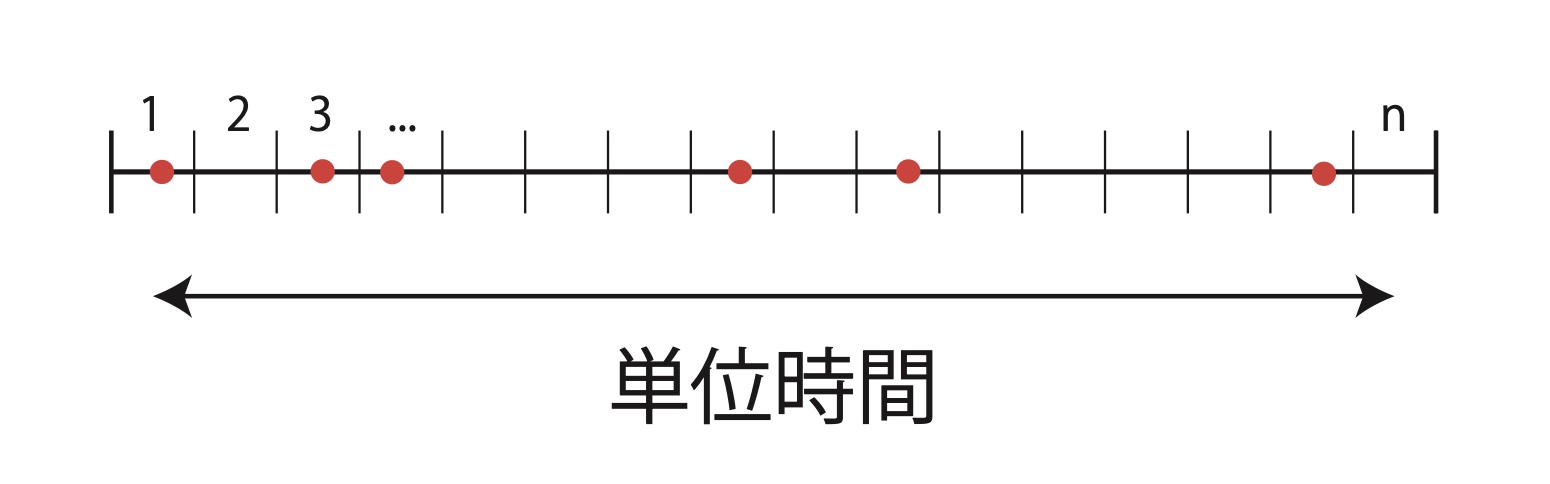
今年、宮城県で交通事故が何回起こるか?とか、ある夜に流れ星が何回流れるか?といった レアなイベントの分布は、ポアソン分布に従う。
ある単位時間に、平均してλ回起こるイベントが、同じ単位時間に k 回起こる確率
を考えよう。ここで単位時間とは一晩とか、1年など、考えているイベントを特徴付けるために 適当に与えられた時間スケールのことをさし、以下ではこれを1とする。
結論を先に述べると、上の確率は
$$
P(\lambda,k)=\frac{\lambda^ke^{-\lambda}}{k!}
$$
となる。例えば、1時間に平均で10の流星が流れる流星群があったとき、15の流星が見れてしまう確率は
$$
P(\lambda,k)=\frac{10^{15}e^{-10}}{15!}=0.034\simeq3.4\%
$$
などというように計算できる。
平均と分散
導出は後回しにして、ポアソン分布\(P(\lambda,k)\)が与えられた時、この分布の平均値と分散を
求めよう。考えるイベントが起こる回数を\(N\)として、その平均を\(\langle N \rangle\)と表す。
\(N\)がポアソン分布に従うなら、定義から\(\langle N \rangle=\lambda\)になっているはずである。
実際に計算してみると
\begin{align*}
\langle N \rangle &= \sum_{k=0}^\infty k P(\lambda,k)\\
&=\sum_{k=1}^\infty k \frac{\lambda^ke^{-\lambda}}{k!}
&=\lambda e^{-\lambda}\sum_{k=1}^\infty \frac{\lambda^{k-1}}{(k-1)!}\\
&=\lambda
\end{align*}
となる。最後に指数関数のマクローリン展開の式を用いた。
次に分散であるが、一応復習しておくと分散とは「平均からのズレの2乗の平均」である。
平均からのずれは\(N-\langle N \rangle\)であるから。これの2乗の平均をとったのが
分散で
$$
\langle(N-\langle N \rangle)^2\rangle=\langle N^2 \rangle – \langle N \rangle^2
$$
右辺で\(\langle N \rangle\)はすでにもとまっているから、\(\langle N^2 \rangle\)を求めればよく
\begin{align*}
\langle N^2 \rangle&=\sum_{k=0}^\infty k^2 P(\lambda,k)\\ &=e^{-\lambda}\sum_{k=1}^\infty k^2 \frac{\lambda^k}{k!} =e^{-\lambda}\sum_{k=1}^\infty \frac{k\lambda^{k}}{(k-1)!}\\ &=e^{-\lambda}\lambda\frac{d}{d\lambda}\left(\sum_{k=1}^\infty \frac{\lambda^{k}}{(k-1)!}\right)\\ &=e^{-\lambda}\lambda\frac{d}{d\lambda}\left(\lambda\sum_{k=0}^\infty \frac{\lambda^{k}}{k!}\right)\\ &=e^{-\lambda}\lambda\frac{d}{d\lambda}(\lambda e^\lambda)=\lambda(\lambda+1) \end{align*}
よって分散は
$$
\langle N^2 \rangle – \langle N \rangle^2=\lambda(\lambda+1)-\lambda^2=\lambda
$$
となる。
ポアソン分布では、平均と分散が等しい。
ショットノイズのSN比
センサーに光子が入ってくるような話では、イベントの平均値が写真の輝度、標準偏差、つまり分散の平方根がノイズに対応する。 ポアソン分布では、平均と分散が等しいので、輝度が\(\lambda$\)なら、その平方根\(\sqrt{\lambda}\)がノイズの大きさになる。
ポアソン分布の導出
上の図に、いま考える単位時間と、その間に起こったイベントを直線と赤丸で示した。この単位時間を ある短い時間間隔で\(n\)等分する。ここで\(n\)をどのくらい大きく取るかというと、短い間隔\(1/n\)の間に イベントが2回起こることは決して無いくらいに大きく取る。
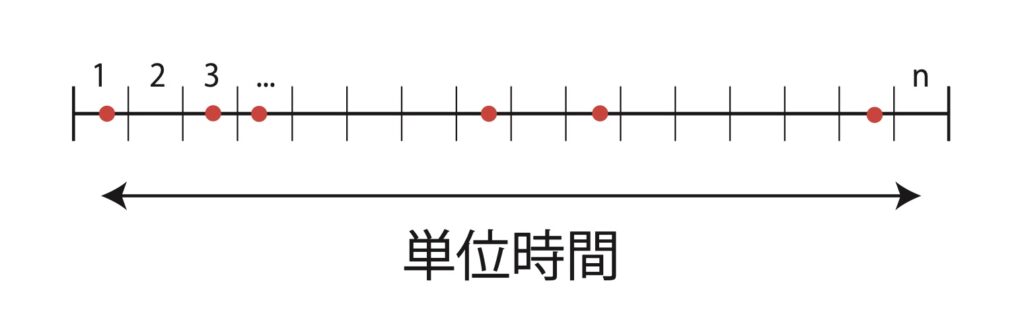
さて、ある時間間隔の間にイベントが起こる確率を\(p\)とすると\(p=\lambda/n\)である。 いま単位時間にイベントが\(k\)回おこる確率を求めたいわけである。 これは確率\(p\)で当たるクジを\(n\)回引いて、\(k\)回あたりを引き当てる確率、と置き換えてこれを考えよう。 これは\(k\)回当たって、\(n-k\)回外れるわけだから
$$
p^k\times(1-p)^{n-k}
$$
である。\(n\)回のくじ引きでどのタイミングで当たってどのタイミングで外れるかは何でも良いので、 図1の赤丸\(k\)個を\(n\)個の箱に割り振る場合の数を掛けて
$$
\frac{n!}{(n-k)!k!}\times p^k\times(1-p)^{n-k}
$$
これが求める確率である。しかしながら元々求めたかった問題に対して、 上の式では\(n\)が余計なパラメータになっていて邪魔である。 ポアソン分布は稀な事象を相手にしているが、 何に比べて稀であるかという話は明確でなくて、それは基準になる時間間隔しだいである。いまイベントが 相当頻繁に起こるとしても、\(n\)を十分に大きく取りさえすれば、その小さな時間間隔で見る限り イベントは「稀」である。そこで\(n\to\infty\)の極限を取ることにしよう。\(p=n\lambda\)を代入してから \(n\to\infty\)として
$$
\lim_{n\to\infty}\frac{n!}{(n-k)!k!}\times \left(\frac{\lambda}{n}\right)^k\times\left(1-\frac{\lambda}{n}\right)^{n-k} =\frac{\lambda^ke^{-\lambda}}{k!}
$$
となる。途中計算は練習問題としよう。